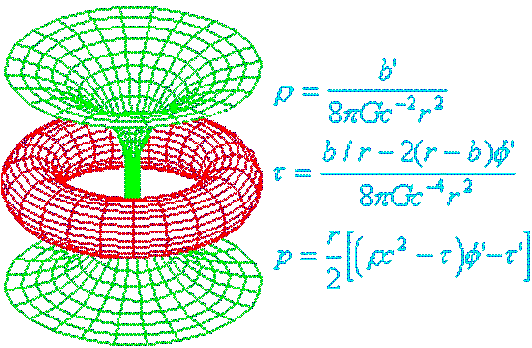
Kerr Black Holes
|
What is a Kerr black hole?
The usual idealised "static" black hole is stationary,
unaccelerated, at an arbitarily-large distance from the observer,
is perfectly spherical, and has a point-singularity at its centre.
When one of these idealised black holes rotates, it gets an extra
property. It's no longer spherically symmetrical , the receding
and approaching edges have different pulling strengths and spectral
shifts, and the central singularity is no longer supposed to be
a dimensionless point.
The equatorial bulge in the event horizon can be deduced in several
ways.
- ... as a sort of centrifugal forces effect. Since it's
possible to model the (distantly-observed) hole as having all
its mass existing as an infinitely-thin film at the event horizon
itself (i.e. where the mass is "seen" to be), you'd
expect this virtual film to have a conventional-looking equatorial
bulge, through centrifugal forces.
- ... as a sort of mass-dilation effect. Viewed from
the background frame, the "moving film" of matter ought
to appear mass-dilated, and therefore ought to have a greater
gravitational effect, producing an increase in the extent of the
event horizon. Since the background universe sees the bh equator
to be moving faster than the region near the bh poles, the equator
should appear more mass-dilated, and should have a horizon that
extends further.
- ... as a shift effect. This tidy ellipsoidal shape
isn't necessarily what people actually see - it's an idealised
shape that's designed to illustrate an aspect of the hole's deduced
geometry independent of the observer's viewing angle. In fact,
the receding and approaching sides of the hole (viewed from the
equator) might appear to have different radii, because it's easier
for light to reach the observer from the approaching (blueshifted)
side than the receding (redshifted) side (these shifts are superimposed
on top of the normal Schwarzchild redshift).
. If we calculate these motion shifts using either the SR shift
assumptions f'/f = (flat spacetime propagation shift)
× root[1 - v²/c²]
or the plain fixed-emitter shift law f'/f
= (c-v)/c, and then treat them as "gravitational",
then by multiplying the two opposing shifts together and rooting
the result, we can get the same averaged dilation factor of f'/f=root(1
- v²/c²) in each case, and by applying the averaged
value, we recreate the same sort of equatorially-dilated shape
that we got in the other two arguments.
Of course, none of these "film" arguments work for a
rotating point, which immediately tells us that the distribution
of matter within a rotating black hole is important, and that
the usual method of treating the actual extent of a body within
the horizon as irrelevant (allowing the use of a point-singularity)
no longer works when the hole is rotating (a rotating hole can't
be said to contain a point-singularity).
In the case of a rotating hole, the simplest state that we can
claim is equivalent to the rotating film of matter for a distant
observer is a ring-singularity.
Notes
- The idea of being able to treat a non-rotating black
hole as either a point-singularity or a hollow infinitely-thin
film is a consequence of the result that the actual mass-distribution
is a "null" property for a black hole, as long as it
is spherically symmetrical. If the mass fits into a Schwarzchild
sphere, the usual static model of a black hole allows the hole's
mass to be point-sized, golfball-sized, or of any size up to the
size of the event horizon.
It's usual to treat all the matter as being compacted to a dimensionless
point, but sometimes it's useful to go to the other extreme and
treat the matter as being at its "observed" position
- as an infinitely-thin film at the event horizon (see Thorne's
membrane paradigm).
- The idea of being able to treat all shifts as being propagation
effects is something that probably ought to be part of GR - in
the context of black holes, the time-dilation effect comes out
as a curved-space propagation effect due the enhanced gravitation
due to kinetic energy. However, there's a slight "political"
problem here, in that GR is supposed to reduce to SR, and SR is
usually interpreted as having Lorentz shifts which are supposed
to be non-gravitational (because allowing the possibility
of gravitational effects upsets the usual SR derivations). A GR-centred
physicist might not have a problem with this approach of treating
all shift effects as being equivalent, a SR-centred one probably
would.
- The "bulginess" of a Kerr black hole is illustrated
on p.293 of the Thorne book (fig
7.9). Thorne says that the effect of the spin on the horizon shape
was discovered Larry Smarr in 1973.
 Back to Blackhole Page.
Back to Blackhole Page.
